1. 两军问题无解
由于传递确认消息的信使与传递原始消息的信使一样,都可能被俘虏而丢失消息,即使双方不断确认已收到对方的上一条消息,也无法确保已与对方达成共识。
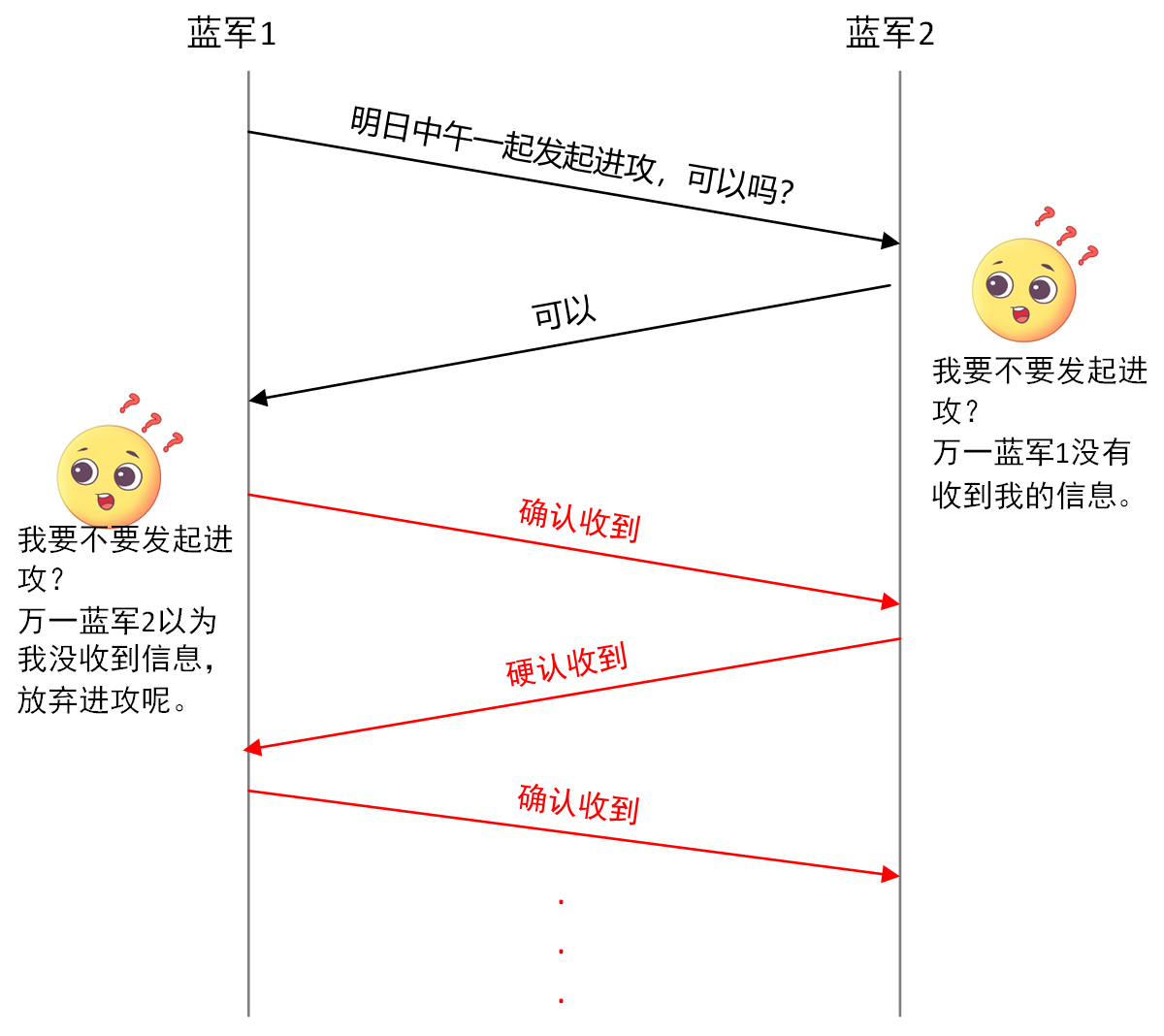
2. 证明
E. A. Akkoyunlu、K. Ekanadham和R. V. Huber首次提到两军问题(但以两组黑帮表示通信双方),并证明问题无解。论文如下:
- Akkoyunlu, Eralp A. et al. “Some constraints and tradeoffs in the design of network communications.” Proceedings of the fifth ACM symposium on Operating systems principles (1975): n. pag.
- 论文PDF
或者看维基百科上面的证明:
(1) For deterministic protocols with a fixed number of messages Because this protocol is deterministic, suppose there is a sequence of a fixed number of messages, one or more successfully delivered and one or more not. The assumption is that there should be a shared certainty for both generals to attack.
Consider the last such message that was successfully delivered. If that last message had not been successfully delivered, then one general at least (presumably the receiver) would decide not to attack. From the viewpoint of the sender of that last message, however, the sequence of messages sent and delivered is exactly the same as it would have been, had that message been delivered.
Since the protocol is deterministic, the general sending that last message will still decide to attack. We've now created a situation where the suggested protocol leads one general to attack and the other not to attack—contradicting the assumption that the protocol was a solution to the problem.
(2) For nondeterministic and variable-length protocols A non-deterministic protocol with a potentially variable message count can be compared to an edge-labeled finite tree, where each node in the tree represents an explored example up to a specified point. A protocol that terminates before sending any messages is represented by a tree containing only a root node. The edges from a node to each child are labeled with the messages sent in order to reach the child state. Leaf nodes represent points at which the protocol terminates.
Suppose there exists a non-deterministic protocol P which solves the Two Generals' Problem. Then, by a similar argument to the one used for fixed-length deterministic protocols above, P' must also solve the Two Generals' Problem, where the tree representing P' is obtained from that for P by removing all leaf nodes and the edges leading to them.
Since P is finite, it then follows that the protocol that terminates before sending any messages would solve the problem. But clearly, it does not. Therefore, a nondeterministic protocol that solves the problem cannot exist.